Discrete Viscous Threads

Miklós Bergou, Basile Audoly, Etienne Vouga, Max Wardetzky, and Eitan Grinspun

Abstract

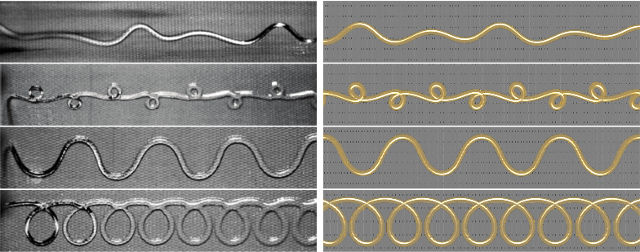
We present a continuum-based discrete model for thin threads of viscous fluid by drawing upon the Rayleigh analogy to elastic rods, demonstrating canonical coiling, folding, and breakup in dynamic simulations. Our derivation emphasizes space-time symmetry, which sheds light on the role of time-parallel transport in eliminating — without approximation — all but an O(n) band of entries of the physical system's energy Hessian. The result is a fast, unified, implicit treatment of viscous threads and elastic rods that closely reproduces a variety of fascinating physical phenomena, including hysteretic transitions between coiling regimes, competition between surface tension and gravity, and the first numerical fluid-mechanical sewing machine. The novel implicit treatment also yields an order of magnitude speedup in our elastic rod dynamics.

Download

"Discrete Viscous Threads"
Miklós Bergou, Basile Audoly, Etienne Vouga, Max Wardetzky, Eitan Grinspun
ACM Transactions on Graphics (SIGGRAPH) 2010
[PDF] [bib] [Video]