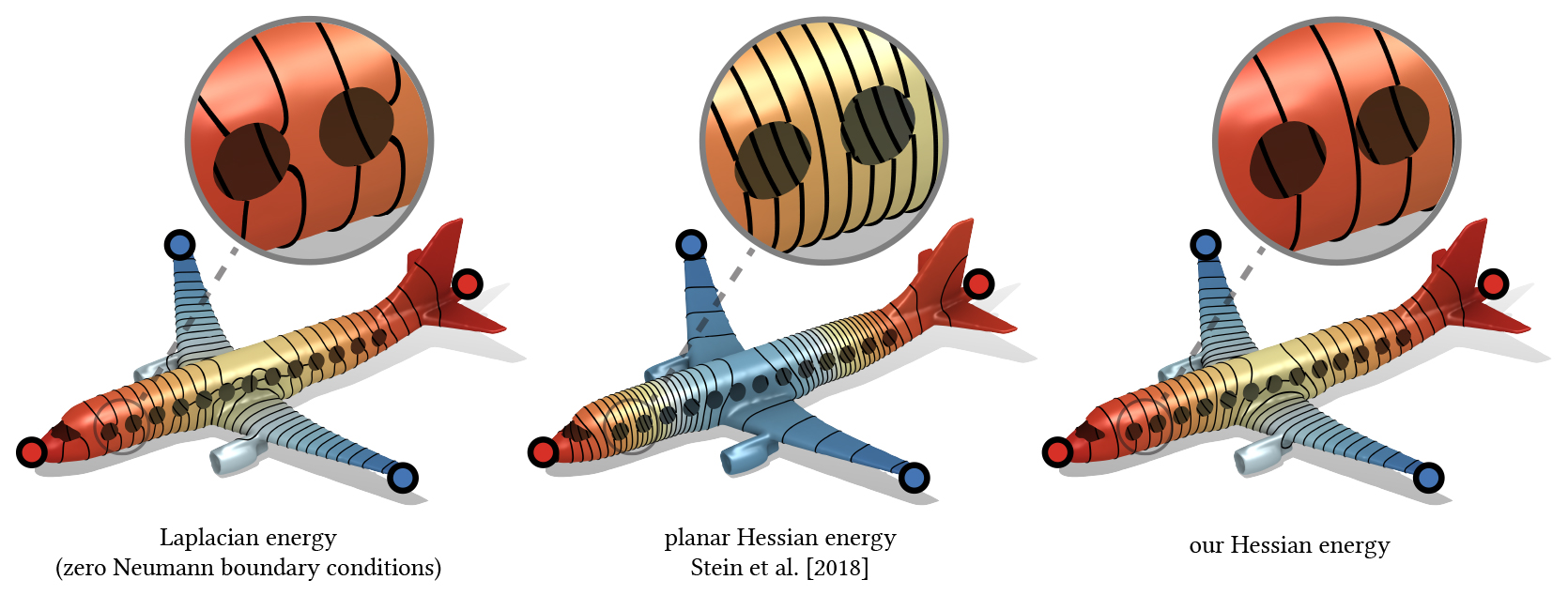

Current quadratic smoothness energies for curved surfaces either exhibit distortions near the boundary due to zero Neumann boundary conditions, or they do not correctly account for intrinsic curvature, which leads to unnatural-looking behavior away from the boundary. This leads to an unfortunate trade-off: one can either have natural behavior in the interior, or a distortion-free result at the boundary, but not both. We introduce a generalized Hessian energy for curved surfaces, expressed in terms of the covariant one-form Dirichlet energy, the Gaussian curvature, and the exterior derivative. Energy minimizers solve the Laplace-Beltrami biharmonic equation, correctly accounting for intrinsic curvature, leading to natural-looking isolines. On the boundary, minimizers are as-linear-as-possible, which reduces the distortion of isolines at the boundary. We discretize the covariant one-form Dirichlet energy using Crouzeix-Raviart finite elements, arriving at a discrete formulation of the Hessian energy for applications on curved surfaces. We observe convergence of the discretization in our experiments.
@article{10.1145/3377406,
author = {Stein, Oded and Jacobson, Alec and Wardetzky, Max and Grinspun, Eitan},
title = {A Smoothness Energy without Boundary Distortion for Curved Surfaces},
year = {2020},
issue_date = {March 2020},
publisher = {Association for Computing Machinery},
address = {New York, NY, USA},
volume = {39},
number = {3},
issn = {0730-0301},
url = {https://doi.org/10.1145/3377406},
doi = {10.1145/3377406},
journal = {ACM Trans. Graph.},
month = mar,
articleno = {Article 18},
numpages = {17},
keywords = {interpolation, Laplacian, biharmonic, Geometry, smoothing, Hessian, curvature} }This work is funded in part by the National Science Foundation Awards CCF-17-17268 and IIS-17-17178. This research is funded in part by NSERC Discovery (RGPIN2017-05235, RGPAS-2017-507938), the Canada Research Chairs Program, the Fields Centre for Quantitative Analysis and Modelling and gifts by Adobe Systems, Autodesk and MESH Inc. This work is partially supported by the DFG project 282535003: Geometric curvature functionals: energy landscape and discrete methods. We thank Anne Fleming, Henrique Maia and Peter Chen for proofreading.